The Unseen Shapes of Reality: Exploring the Dimensions Beyond Our Everyday Experience
When we glance around our immediate environment, it’s easy to perceive the world as flat. After all, a simple map, a flat representation, suffices for navigating cities and understanding spatial relationships. This intuitive sense of flatness is what once led people to believe the Earth itself was a planar surface. However, we now know that reality is far more complex. We inhabit the surface of a vast sphere, akin to a giant, slightly bumpy beach ball – planet Earth.
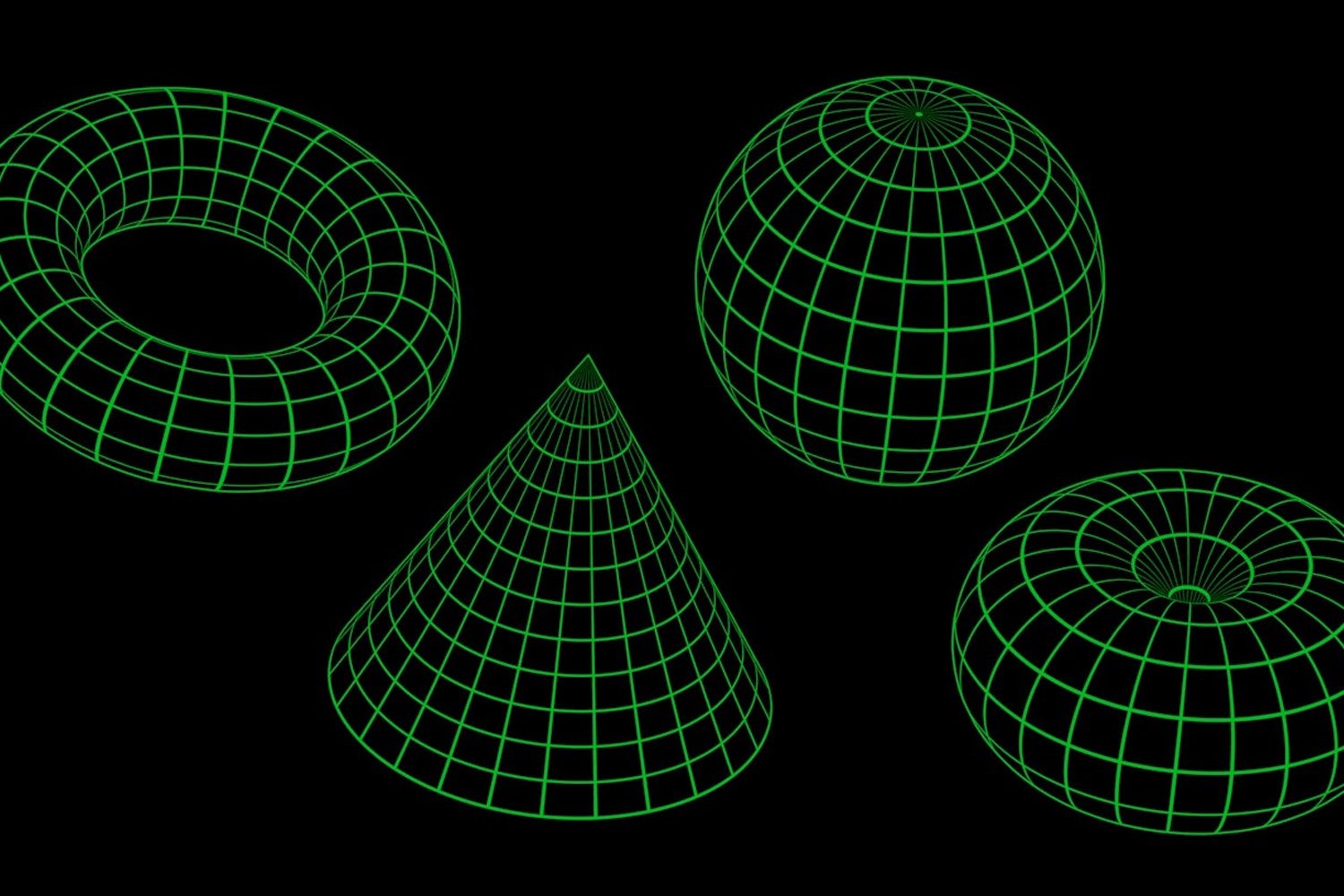
The surface of this sphere, like a flat plane, represents a two-dimensional (2D) space. On either, you can move in two independent directions, typically described as north-south or east-west. But the question arises: what other kinds of spaces might exist around us? Are there other 2D surfaces beyond planes and spheres? The answer, surprisingly, is yes. Consider the surface of a doughnut, a mathematical object known as a torus. It’s another example of a 2D space, distinct in its geometric properties from both the plane and the sphere.
This is where geometric topology, the area of mathematics I study, comes into play. We explore all possible spaces, irrespective of their dimension. Whether the goal is to design robust sensor networks, analyze large datasets, or even utilize origami for deploying satellites in space, the underlying principles often stem from the realm of topology.
Our everyday perception paints the universe as a three-dimensional (3D) space, similar to how the Earth’s surface appears as a 2D space. However, just as the Earth is actually a sphere, the universe as a whole may possess a more intricate structure, perhaps resembling a giant 3D analogue of a beach ball or some other, even more perplexing configuration.
While topology isn’t essential for simply recognizing that we live on a spherical object, understanding the possibilities for 2D spaces proves remarkably useful. Over a century ago, mathematicians exhaustively classified all potential 2D spaces and identified their defining characteristics. This level of understanding provides a foundation for exploring higher dimensions.
In recent decades, significant strides have been made in comprehending the landscape of possible 3D spaces. While we haven’t achieved the same complete understanding as we have for 2D spaces, our knowledge is extensive. With this accumulated knowledge, physicists and astronomers can probe the actual 3D space we inhabit, seeking to unravel the universe’s true shape.
The answer to this fundamental question remains elusive, but the potential solutions are both captivating and unexpected. And the possibilities become exponentially more complex when we introduce time as an additional dimension.
Think about describing the position of a comet in space. You need four numbers: three coordinates to pinpoint its spatial location and one to specify the precise moment in time. These four numbers together constitute a point in a four-dimensional (4D) space. Now, we can begin to explore the realm of possible 4D spaces and investigate which one accurately describes the universe we experience.
At this stage, it might seem pointless to contemplate spaces with more than four dimensions, as that appears to be the upper limit for describing our universe. However, string theory, a prominent branch of physics, proposes that the universe could possess far more than four dimensions.
Beyond theoretical physics, contemplating higher-dimensional spaces has practical applications, such as robot motion planning. Imagine designing a system for three robots to navigate a factory floor. To describe the position of each robot, we use two coordinates (x and y) relative to a grid on the floor. Since each robot requires two coordinates, we need six numbers to fully describe the position of all three robots. These possible robot configurations can be visualized as a 6D space.
As we increase the number of robots, the dimensionality of the space grows accordingly. Moreover, factoring in constraints like the location of obstacles further complicates the space. To tackle such problems effectively, we need the tools and techniques to study high-dimensional spaces.
Countless other scientific problems involve high-dimensional spaces, ranging from modeling the trajectories of planets and spacecraft to discerning the inherent “shape” of massive datasets. In many areas of scientific endeavor, dealing with numerous variables requires thinking in terms of high-dimensional spaces.
Another area of focus for topologists is how one space can be embedded within another. Consider a knotted loop of string. This loop represents a one-dimensional (1D) space residing within the three-dimensional (3D) space of your room. These looped and intertwined strings are known as mathematical knots.
The study of knots originated in physics but has evolved into a core area of topology. Knots are critical for understanding the geometry of 3D and 4D spaces and exhibit subtle and complex structures that researchers are still exploring.
Furthermore, knots have diverse applications spanning string theory in physics, DNA recombination in biology, and chirality in chemistry. Their properties are proving invaluable across a wide range of scientific disciplines.
Geometric topology is a rich and intricate field, with an abundance of unsolved questions surrounding the nature of spaces. For example, the smooth 4D Poincaré conjecture asks what the "simplest" closed 4D space is. The slice-ribbon conjecture, on the other hand, seeks to understand how knots in 3D spaces relate to surfaces in 4D spaces.
Topology is currently a valuable tool in science and engineering. Unraveling the mysteries of spaces across all dimensions will undoubtedly be essential for understanding the universe we inhabit and for tackling real-world problems. By continuing to investigate these mathematical frontiers, we can unlock new insights into the fundamental nature of reality and pave the way for future innovations.
